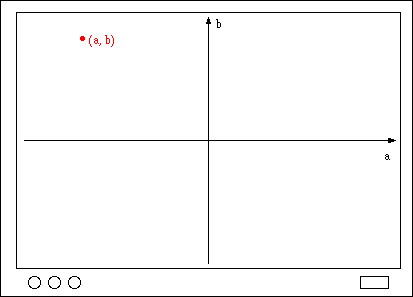
Figur 4.1
Som vi ser ut fra definisjonen av M over må vi avgjøre om et gitt punkt c gjør at f(z) går mot uendelig for å finne ut av om det er med i M eller ikke.
Ved plotting av Mandelbrot-mengden setter vi av den reelle verdien langs x-aksen og den imaginære verdien langs y-aksen.
Før vi går videre kan det være nødvendig med en kort beskrivelse av hvordan en datamaskinskjerm er bygd opp. Bildet består av en rekke små punkter, kalt piksler. Hvor mange piksler vi har bestemmer skjermens oppløsning. Jo flere piksler, jo høyere oppløsning. Vanlige oppløsninger er:(horisontalt x vertikalt)
Skjermen kan oppfattes som et plan hvor hver piksel representerer et tallpar (a, b). a og b er begrenset av området vi ønsker å plotte Mandelbrot-mengden for.

Dette tallparet gir oss verdien for c. For punktet i øverste venstre hjørne på figuren:
En piksel i horisontal retning vil ha c-verdi:
En piksel i vertikal retning blir på tilsvarende måte:
dA og dB er gitt ved:
dB = (bmax - bmin) / vertikaloppløsning
Av dette ser vi at jo høyere oppløsning, jo mer nøyaktig vil plottet av M bli.
Disse c-verdiene plugges inn i funksjonen f(z) som deretter itereres for å finne ut om den går mot uendelig eller ikke. Da f0(z) = 0 får vi
| n | fn(z) |
| 0 | 0 |
| 1 | 02 + (a + ib) |
| 2 | (a + ib)2 + (a + ib) |
| 3 | [(a + ib)2 + (a + ib)]2 + (a + ib) |
Pseudokode for det ovenstående:
FOR HVER piksel
GJENTA
KALKULER fn(z) = (fn-1(z))2 + c
n = n + 1
SÅ LENGE fn(z) < uendelig
PLOT piksel
Når er så f(z) = uendelig? Det er det(selvsagt) desverre ikke mulig å finne ut. Det kan imidlertid vises at Mandelbrot-mengden liggen innenfor |c| <= 2 og at dersom |z| > 2 så divergerer omløpsbanen.
Bevis:
|
Dersom |z| > 2 så er |z2 + c| >= |z2| - |c| > 2|z| - |c| Dersom |z| >= |c| så er 2|z| - |c| > |z| Så om |z| > 2 og |z| >= |c| er |z2 + c| > |z| og rekken er stigende. |
f(z) går altså mot uendelig når fn(z) > 2.
Fra den geometriske betraktningen i fig. 3.2, ser vi at verdien av fn(z) er lik lengden av vektoren gitt ved funksjonens reelle og imaginære deler. Av dette følger
Programmet kan nå skrives som
FOR HVER piksel
GJENTA
KALKULER fn(z) = fn-1(z) + c
Lengde = (fn(z).reell2 + fn(z).imaginær2)1/2
n = n + 1
SÅ LENGE Lengde <= 2
PLOT piksel
Det er en ting vi ikke har tatt med i betraktning enda. Som vi har sett går ikke f(z) mot uendelig for alle verdier av c. For enkelte verdier, f.eks c = 0, vil lengden av vektoren til f(z) aldri kunne bli større enn 2 og programmet vil aldri kunne komme ut av kalkuleringsløkken. For å unngå dette må vi sette en øvre grense for antall iterasjoner. Dersom lengden av vektoren ikke er blitt større enn 2 i løpet av dette antallet iterasjoner antar vi at f(z) ikke går mot uendelig for denne verdien av c og hopper ut av løkken.
FOR HVER piksel
GJENTA
KALKULER fn(z) = fn-1(z) + c
Lengde = (fn(z).reell2 + fn(z).imaginær2)1/2
n = n + 1
SÅ LENGE Lengde <= 2 OG n <= maksimum antall iterasjoner
PLOT piksel
Dette kan vi gjøre om til et virkelig program og plotte Mandelbrotmengden. I Java vil de viktige prosedyrene se slik ut: (Legg merke til at vi gjør en forandring i forhold til koden foran. Istedenfor å sjekke om lengden av svarvektoren er mindre enn eller lik 2, sjekker vi om lengden2 er mindre enn eller lik 4 og slipper dermed å ta kvadratroten. Dette sparer tid.)
minA = -2.00; //(minA, maxB) er øvre venstre hjørne
maxB = 2.00;
maxA = 2.00; //(maxA, minB) er nedre høyre hjørne
minB = -2.00;
maxItereringer = 256;
//dA og dB er endringen i a- og b-verdi fra en piksel til den neste
dA = (maxA - minA) / horisontalOppløsning;
dB = (maxB - minB) / vertikalOppløsning;
for (y = 0; y < vertikalOppløsning - 1; y++) { //Plot linje for linje
for (x = 0; x < horisontalOppløsning - 1; x++) { //Plot hver pixel på linjen
reell = 0; //Setter variablene til null ved start av hver
imaginær = 0; //itereringssyklus
iterering = 0;
do {
gammel_reell = reell; //ta vare på reell verdi fra forrige iterasjon
reell = reell * reell - imaginær * imaginær + (minA + (double)x * dA);
imaginær = 2 * gammel_reell * imaginær + (minB + (double)y * dB);
iterering++;
lengde_Z = reell * reell + imaginær * imaginær;
} while ((lengde_Z <= 4.0) && (iterering <= maxIterering));
} //rof x
} //rof y
if (iterering <= maxIterering) { //Dersom vi hoppet ut av løkken fordi lengde_Z ble større
g.setColor(Color.white); //enn 4 er punktet ikke en del av Mandelbrotmengden og
//vi plotter det med hvit farge.
}
else { //Forlot vi derimot løkken fordi antall itereringer ble større
g.setColor(Color.black); //det maksimale antall tillate, er punktet en del av Mandelbrotmengden
//og vi plotter det med sort farge.
}
g.drawLine(A, B, A, B); //Plot punktet
Hele programmet ligger her og i figur 4.2 ser vi resultatet av programmet. Du kan også kjøre det selv.
 Figur 4.2
Figur 4.2
Vi har tidligere snakket om maksimalt antall iterasjoner. Dette tallet må nødvendigvis ha en innvirkning på hvordan Mandelbrotmengden blir seende ut. I programmet over satte vi maxItereringer = 256. Det betyr at et punkt for hvilket f(z)-vektoren får lengde > 4 etter 257 iterasjoner feilaktig blir med i Mandelbrotmengden. Dette gjelder spesielt i grenseområdet, hvor antall nødvendige itereringer kan bli stort.
Vi kan illustrere dette ved å kjøre det samme programmet med maxIterering satt lik 10. (Kildekode)

Strukturen kan fremdeles gjenkjennes, men vi ser at nå er Mandelbrot-mengden blitt mye større og mer utflytende rundt grensene. Vi vil altså aldri kunne plotte den eksakte Mandelbrot-mengden.
Men så langt ser jo figurene vi får fryktelig kjedelige ut! Hvor er det blitt av alle fargene som vi er vant til å se når vi finner tegninger av Mandelbrot-mengden?
Å fargelegge Mandelbrot-mengden er svært enkelt.
| Alle punkter som bruker det samme antall itereringer på å oppfylle kravet til ikke å være med i M plottes med samme farge. |
Vi modifiserer tegnedelen av programmet over til
if (iterering <= maxIterering) { //Dersom vi hoppet ut av løkken fordi lengde_Z ble større
g.setColor(farge[iterering - 1])); //enn 4 er punktet ikke en del av Mandelbrotmengden og
//vi plotter det med fargen som tilsvarer antall itereringer
//Vi bruker [iterering - 1] da det første elementet
//i en matrise i Java er 0
}
else { //Forlot vi derimot løkken fordi antall itereringer ble større
g.setColor(Color.black); //det maksimale antall tillate, er punktet en del av Mandelbrotmengden
//og vi plotter det med sort farge.
}
g.drawLine(A, B, A, B); //Plot punktet
Fargene definerer vi slik:
| Itereringer | Farge | |
| 1 | Blå | 2 | Lys blå |
| 3 | Mørk grå | |
| 4 | Grå | |
| 5 | Grønn | |
| 6 | Lys grå | |
| 7 | Lilla | |
| 8 | Orange | |
| 9 | Rød | |
| 10 | Rosa | |
| 11 | Gul |
Vi kjører det nye programmet med maxIterering satt lik 11 slik at vi får en farge pr. mulig itereringsverdi. (Kildekode)
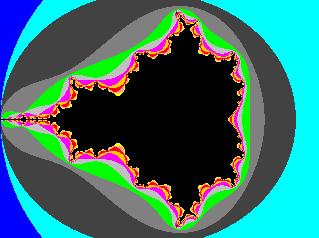
Nå kan vi tydelig se hvordan punkter med samme itereringsverdi legger seg i regelmessige bånd. Vi ser også at jo nærmere vi kommer grensen til Mandelbrot-mengden, jo flere itereringer kreves det før f(z) for punktet går mot uendelig.