3.0 Mandelbrot-mengden

Mandelbrot-mengden er kanskje den mest berømte representant for den fraktale geometrien. I dette avsnittet vil jeg se på den matematiske bakgrunnen for mengden og hvordan den fremkommer.

Grunnlaget for Mandelbrot-mengden er den enkle ikke-lineære funksjonen

f(z) = z2 + c, hvor z og c er komplekse tall.

Dvs.

z = x + iy, hvor i = -11/2 og x og y er reelle tall

Ved å sette f(z) = u + iv og c = a + ib får vi

z2 + c = u + iv

(x + iy)2 + (a + ib) = u + iv

x2 + 2xiy - y2 + a + ib = u + iv

(x2 - y2 + a) + i(2xy + b) = u + iv

Nå har vi fått et fullstendig uttrykk for f(z)

f(z) = (x2 - y2 + a) + i(2xy + b)


Fig. 3.1

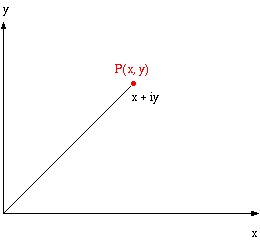
Komplekse tall kan i planet representeres geometrisk ved å sette x-aksen som den reelle aksen og y-aksen som den imaginære aksen. Det komplekse tallet f(z) kan da identifiseres som et punkt P i planet. Dette punktet vil ha koordinatene (u, v), der

u = x2 - y2 + a, v = 2xy + b

Mandelbrot-mengden genereres ved en prosess kalt iterering: en stadig gjentakelse av funksjonen. Argumentet til funksjonen er resultatet av den forrige itereringen, dvs.

fn(z) = f(fn-1(z))

Hver ny iterasjon gir opphav til et tallpar

Pn = (un, vn)

der

un = u2n-1 - v2n-1 + a, vn = 2un-1vn-1 + b

Dette gir oss punktrekken

P0 = z, P1 = z2 + c, ...., Pn = fn(z)

Som vi i så i utledningen av uttrykket for u og v over, vil denne punktrekken avhenge både av z = x + iy og av det komplekse tallet c. Vi velger å holde c fast og undersøker hva som skjer med funksjonen når vi endrer startverdien(seed) av z. Denne startverdien kalles z0. Når vi iterer får vi da

z1 = z02 + c
z2 = z12 + c
z3 = z22 + c
z4 = z32 + c
osv.

Den resulterende tallrekken kalles omløpsbanen til z0 ved iterasjon av z2 + c. Et viktig spørsmål innen fraktal matematikk er hva som skjer med omløpsbanene? Er de sykliske? Konvergerer eller divergerer de?

For Mandelbrot-mengden er z0 definert lik 0. Til grunn for denne definisjonen ligger at 0 er den kritiske verdien til funksjonen, dvs. punktet hvor d/dz[f(z)] = 0 for f(z) = z2 + c. For en annen funksjon er det mulig z0 må endres. For g(z) = z2 + z vil d/dz[g(z)] = 2z + 1. Kritisk verdi, og startverdi, for g(z) blir da 0.5.

Omløpsbaner for noen verdier av c:

zn c = i c = 2i c = -i c = 0
z00000
z1i2i-i0
z2-1 + i-4 + 2i-10
z3-i12 - 4i1 - i0
z4-1 + i-52 - 334i-i0

Tabell 3.1

Vi ser at for c = i er omløpsbanen syklisk med periode 2, for c = 2i går den mot uendelig, for c = -i er den syklisk med periode 3, mens for c = 0 er den statisk.

Heri ligger Mandelbrot-mengdens dualitet:

Ved iterering av z2 + c vil omløpsbanen for z0 = 0 enten gå mot uendelig eller ikke.
Går den ikke mot uendelig kan den oppføre seg statisk, syklisk eller kaotisk.

Herav følger også Mandelbrot-mengdens definisjon:

Mandelbrot-mengden M består av alle de komplekse c-verdier for hvilke den tilhørende omløpsbanen for z0 = 0 under z2 + c ikke går mot uendelig.

Av tabell 3.1 ser vi da at c = i, c = 0 og c = -i er en del av Mandelbrot-mengden, mens c = 2i ikke er det.

Figuren i innledningen viser en grafisk representasjon av Mandelbrot-mengden. I det neste avsnittet vil jeg se på hvordan denne fremkommer og hva slags informasjon som kan leses ut fra den. Parallellt med dette vil jeg utvikle et Java-program som kan generere bilder av Mandelbrot-mengden.

[Neste: 4.0 Generering av Mandelbrot-mengden vha. datamaskinen]   [Forrige: 2.0 Hva er en fraktal?]