Fraktaler

2.0 Hva er en fraktal?

Ordet fraktal ble første gang brukt av den polsk-amerikanske matematikeren Benoit Mandelbrot i hans bok The Fractal Geometry of Nature som kom ut i 1983.

Han definerer en fraktal som

en ujevn eller fragmentert geometrisk form som kan deles opp i flere subdeler, som hver er(idet minste tilnærmet) en mindre kopi av det hele. Figurene er selv-similære og uavhengige av skalaen de betraktes på. [Taylor]

Matematisk definerer han fraktaler som

et punktmengde X hvis Hausdorff dimensjon h(X) ikke er heltallig. [Crilly, et. al.]

Det finnes en mengde geometriske figurer som er fraktaler, f.eks. Sierpinski-triangelet, von Koch-kurven og Mandelbrot-mengden. Fraktaler har også vist seg å beskrive mange naturlige fenomen, så som skyer, fjell, stormer, planetenes baner, sosioøkonomiske mønster, musikk mm. Dette er fenomener som ikke lar seg beskrive ved klassisk, eller euklidsk, geometri.

Hva ligger det så i disse to definisjonene?

2.1 Selv-similaritet

Begrepet selv-similaritet er viktig for forståelsen av fraktaler. Ideen bak kan best beskrives ved hjelp av et eksempel: Sierpinski-trekanten.

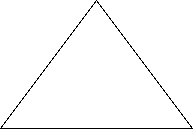
Utgangspunktet for konstruksjonen av Sierpinski-trekanten er en vanlig trekant.

Fig. 2.1

Forbind sidenes midtpunkter med hverandre og fjern den midterste trekanten.

Fig. 2.2

Innesluttet i den originale trekanten har vi nå 3 mindre trekanter.

Dersom vi nå gjør det samme for hver av de nye trekantene får vi følgende figur.

Fig. 2.3

En gang til...

Fig. 2.4

Og en siste gang...

Fig 2.5

På denne måten kan vi teoretisk sett fortsette i det uendelige.

Vi ser at trekantene i hjørnene vil være nøyaktig like hele trekanten om de forstørres to ganger. Trekanten er selv-similær.

2.2 Fraktalers dimensjon

Geometriundervisningen i skolen er plassert i det euklidske/newtonske univers. Den omhandler null-, en-, to-, eller tre-dimensjonale figurer.

Fig. 2.6

Et punkt har dimensjon 0: vi sier det er dimensjonsløst.

Fig. 2.7

En linje har dimensjon 1: Et vilkårlig punkt A på linjen kan beskrives ved hjelp av ett tall, f.eks. avstanden fra starten av linjestykket.

Fig. 2.8

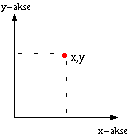
Et plan har dimensjon 2: For å kunne beskrive et vilkårlig punkt B trenger en to tall, en x-koordinat og en y-koordinat.

Fig. 2.9

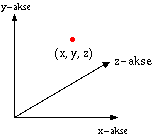
Den newtonske beskrivelsen av universet vi lever i er tredimensjonal: Et vilkårlig punkt beskrives av tre tall, en x-koordinat, en y-koordinat og en z-koordinat.

Ofte trenger vi mer enn tre tall for å beskrive en situasjon på en tilfredstillende måte. Det kan være viktig å registrere når noe skjer, i tillegg til hvor det skjer. Da trenger vi 4 koordinater: x, y, z og t(tid). Hendelsen er 4-dimensjonal. En partikkels bane i tiden beskrives ved hjelp av x, y, z og t, men i tillegg må vi ha med v_x, v_y, v_z for å angi hastighetens komponenter. Beskrivelsen er altså 7-dimensjonal.

Det har imidlertid vist seg at fraktaler ikke alltid lar seg beskrive ved hjelp av en n-dimensjonal betraktning, hvor n er et heltall. For å illustrere dette vil jeg se på von Koch-kurven.

von Koch-kurvens dimensjon

von Koch-kurven konstrueres med utgangspunkt i et linjestykke med lengde 1. Den midtre 1/3 av linjen fjernes og erstattes av to linjer med lengde 1/3. Denne prosessen gjentas gang på gang. Etter 3 repetisjoner får vi en figur som vist nedenfor.

Fig. 2.10

For hver gang prosessen gjentas, observerer vi at kurvens lengde øker med 4/3

Steg	Kurvens lengde
0	1
1	4/3
2	16/9
3	64/27
4	256/81

Tabell 2.1

Vi ser at jo flere steg vi gjennomfører jo lengre blir den resulterende kurven. Den fullførte von Koch-kurven(resultatet av et uendelig antall steg) vil altså være uendelig lang.

Kurven er også selv-similær; den inneholder et uendelig antall perfekte miniatyr-kopier av seg selv. Da kurven er uendelig lang, er også enhver miniatyr-kopi uendelig lang. Konsekvensen av dette er at avstanden mellom to vilkårlige punkter på kurven er uendelig lang.

Hva slags betydning har så dette for von Koch-kurvens dimensjon?

Ut fra fig. 2.10 kan det se ut som om kurven er 1-dimensjonal. Som sagt over kan et punkt på en 1-dimensjonal kurve angis ved å oppgi avstanden til kurvens startpunkt. Men i dette tilfellet er ikke det mulig, da avstanden mellom to punkter er uendelig lang og dermed ikke lar seg tallfeste.

Kurven fyller heller ikke planet den befinner seg i, så den kan ikke være 2-dimensjonal.

von Koch-kurvens dimensjon ser dermed ut til å ligge et sted mellom disse to. Den er ikke heltallig.

2.2.1 Beregning av fraktalers dimensjon

For å finne en metode for å beregne en fraktals dimensjon kan en ta utgangspunkt i normale euklidske/newtonske geometriske figurer: et linjestykke(dimensjon 1), et plan(dimensjon 2) og en kube(dimensjon 3).

Alle disse figurene deler en egenskap: de er selv-similære.

Deler vi et linjestykke opp i 2 like deler vil hver del være halvparten så lang som det hele. Deler vi det samme linjestykket opp i 3 deler vil hver del være 1/3 så lang som det hele. 4 deler gir lengde lik 1/4 av det hele.

Et linjestykke kan deles opp i N selv-similære stykker av lik lengde, hvert med skaleringsfaktor k = 1/N.

Fig. 2.11

En firkant kan deles opp i 4 like deler med skaleringsfaktor 1/2, 9 like deler med skaleringsfaktor 1/3, osv.

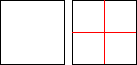
Et plan kan deles opp i N selv-similære stykker av likt areal, hvert med skaleringsfaktor k = 1/N^1/2.

Fig. 2.12

En kube kan deles opp i 8 like deler med skaleringsfaktor 1/2, 27 like deler med skaleringsfaktor 1/3, osv.

En kube kan deles opp i N selv-similære deler av likt volum, hver med skaleringsfaktor k = 1/N^1/3.

Fig. 2.13

Ut fra dette finner vi at det generelle forholdet mellom N og k er

k = 1/N^1/D, der D er figurens dimensjon.

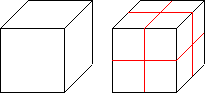
En liten omskrivning gir

N = (1/k)^D

Nå kan D finnes ved hjelp av logaritmer

N = (1/k)^D
log(N) = log((1/k)^D)
log(N) = D * log(1/k)
D = log(N)/log(1/k)

Vi har nå et generelt uttrykk for dimensjonen til enhver selv-similær figur og kan bl.a. finne dimensjonene til de to fraktalene vi har sett på tidligere, Sierpinski-trekanten og von Koch-kurven.

Av fig. 2.5 fremgår det at Sierpinski-trekanten har N = 3 selv-similære kopier ved skaleringsfaktor k = 1/2. Dette gir:

D = log(3)/log(2) = 1.58

von Koch-kurven har N = 16 selvsimilære kopier ved skaleringsfaktor k = 1/9. Dette gir:

D = log(16)/log(9) = 1.26

Denne metoden fungerer svært bra for geometriske figurere som er strengt selv-similære. Det er imidlertid svært få (relativt sett) figurer som oppfyller dette kravet. Den tyske matematikeren Felix Hausdorff har imidlertid kommet frem til en definisjon av D(heretter referert til som D_(H)) som er gyldig for alle geometriske figurer.

Hausdorff benytter begrepet 'nabolag', som betegner et lite, regulært område sentrert om et gitt punkt. I 1 dimensjon vil nabolaget være et lite linjestykke, i 2 dimensjoner en sirkel, i 3 dimensjoner en kule.

Dekk figuren hvis dimensjon vi ønsker å finne med nabolag av en bestemt størrelse. Anta at vi trenger N₁ nabolag for dekke figuren slik at hvert av punktene ligger inne i ett av nabolagene. Gjør det samme en gang til, men med nabolagene skalert med faktor k. Denne gang trenger vi N₂ nabolag. Antall nabolag N₁ og N₂ vil være avhengig av størrelsen på nabolagene og figurens utseende. Det finnes ikke noe eksakt forhold, men dersom nabolagene er svært små vil det finnes en grenseverdi for N₂/N₁ som avhenger av skaleringsfaktoren k. Hausdorffs definisjon av dimensjonen D_(H) blir da:

N₁/N₂ = (1/k)^D_(H)
D_(H) = log(N₂/N₁) / log(1/k)

For en fraktal vil det selvsagt ikke være så enkelt å bestemme det nøyaktige nabolaget, men i praksis kan det erstattes med en annen liten regulær figur, som f.eks. en firkant. Dette vil gi et godt estimat for den virkelige verdien av D_(H).

Eksempel 1: Estimering av D_(H) for von Koch-kurven

Fig. 2.14

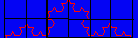
Vi ser at for å dekke kurven trenger vi 3 store kvadrat, mens vi trenger 8 kvadrat med skaleringsfaktor 1/2. Etter dette blir dimensjonen for Koch-kurven:

D_(H) = log(8/3)/log(1/(1/2)

D_(H) = 1.415

Dette samsvarer ikke så godt med svaret vi fikk tidligere, men skyldes vel at rutenettet vi bruker er for grovt.

Eksempel 2: Estimering av D_(H) for kystlinje

Fig. 2.15

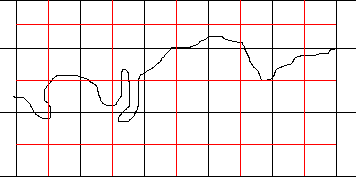
Kystlinjen dekkes av 9 store kvadrat, mens vi trenger 17 små kvadrat med skaleringsfaktor 1/2. Kystlinjens dimensjon blir dermed:

D_(H) = log(17/9)/log(1/(1/2)

D_(H) = 0.92

[Neste: 3.0 Mandelbrot-mengden] [Forrige: 1.0 Innledning]