5.0 En liten sightseeing i Mandelbrot-mengden

Programmet som har tegnet bildene i denne delen av oppgaven er en del forskjellig fra de vi har brukt tidligere. Kildekoden finner du her. Max antall itereringer er satt til 256 og til hver iterering svarer en farge. (Fargene genereres på slump, så fargene vil ikke være de samme om programmet kjøres to ganger.) Det er i tillegg lagt til rutiner for å kunne kalle programmet med ulike verdier for vertikal og horisontal oppløsning samt ulike plotteområder.

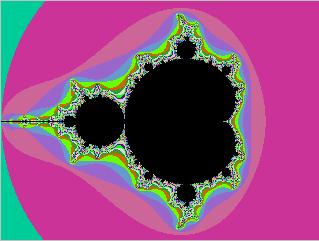
Først ser vi på Mandelbrot-mengden slik den ser ut når den plottes med det nye programmet

Fig. 5.1

Vi kan zoome inn i mengden ved å velge et mindre plotteområde. Vi kan undersøke 'hodet' til M. (Dette plottet tar lang tid! Hvorfor tar akkurat dette plottet så lang tid? Svar)

Fig. 5.2
Et av kravene til en fraktal var at den skulle være selv-similær. Så langt har vi ikke sett noen tegn på at M er det. M er imidlertid selvsimilært i enkelte punkter. Studerer vi figur 5.2 ser vi et sort område ute mot venstre side. Zoomer vi inn på dette får vi følgende bilde:

Fig. 5.3
Slike mini-Mandelbrot finnes det flere av i Mandelbrot-mengden. Bl.a. finner vi en ved minA = -0.268, maxB = -0.958, maxA = -0.068, minB = -1.108

Fig. 5.4
Her kan vi se enda to mini-Mandelbrotmengder; en oppe i venstre hjørne og en nede til høyre.
Det finnes ennå mange fenomener å studere i Mandelbrot-mengden, men jeg velger å stoppe her. Et fraktalgenereringsprogram med bedre zoomingsmuligheter, så som Fractint, vil la deg fortsette utforskningen av Mandelbrotmengden. PGD's Quick Guide to the Mandelbrot Set kan gi deg tips om hvor det finnes interessante ting å se.

[Forrige: 4.0 Generering av Mandelbrot-mengden vha. datamaskinen] [Neste: 6.0 Litteraturliste]