3.0 Noen geometriske betraktninger

3.1 Grovinndeling

Mathesongården kan deles inn i rektangler: enten horisontalt eller vertikalt.

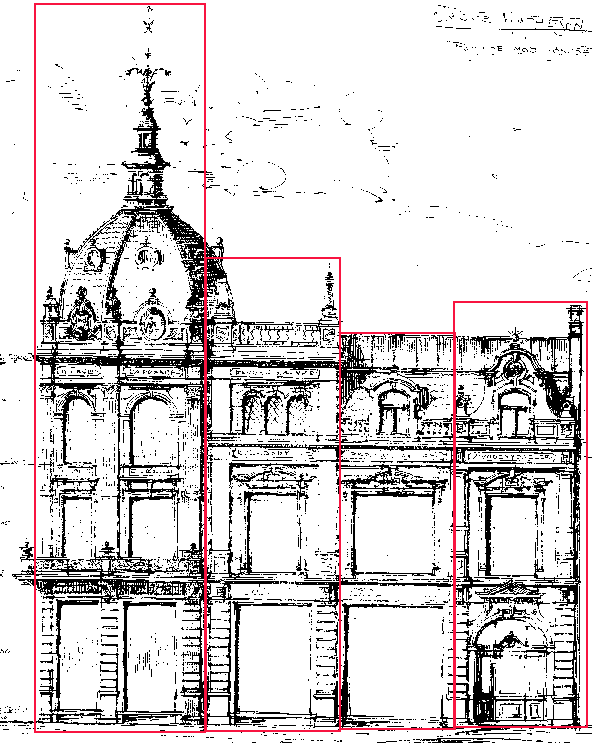
Deler vi bygget vertikalt får vi følgende 4 deler:

Figur 1

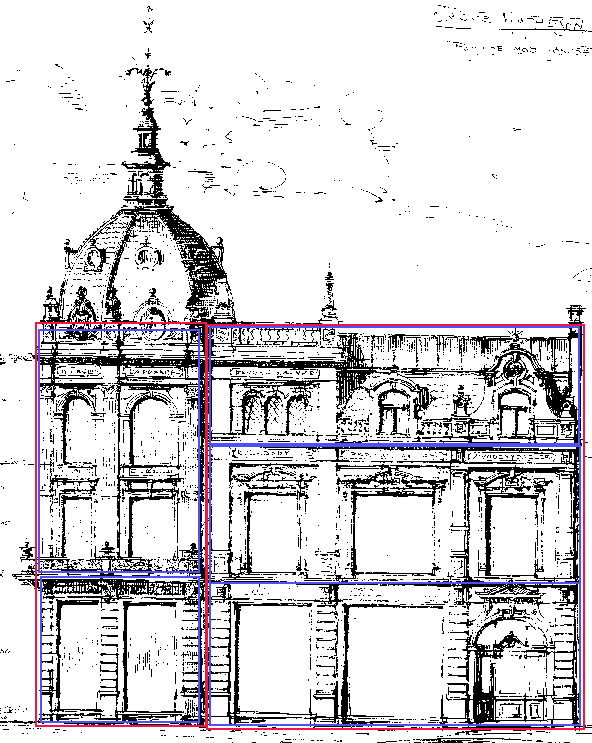
Horisontalt kan vi dele det i to hoveddeler(markert med rødt). Den fremre kan deles i to subdeler(markert med blått) og den bakre kan deles i tre. (Kuppelen untatt).

Figur 2

3.2 Det gyldne snitt i Mathesongården

Det gyldne snitt viste seg å være meget fremtredene i Mathesongårdens geometri. Vi vil først se litt på teorien bak dette spesielle snittet.

3.2.1 Teori

Definisjonen av det gyldne snitt er

Hvis linjestykket AB er delt i et punkt C slik at

(a+b)/a = a/b

sies C å dele AB i det gyldne snitt

Figur 3

Sagt på en annen måte: Forholdet mellom hele linjestykket (a + b) og den lengste del a er lik forholdet mellom den lengste del(a) og den korteste del(b).

Det kan vises at C deler linjestykket AB i det gyldne snitt nettopp når

a/b = 1 + (5^1/2) / 2

Tallet a/b betegnes phi og får verdien 1.618034.....

Et rektangel hvor forholdet mellom lengste og korteste side er lik phi kalles et gyldent rektangel.

3.2.2 Det gyldne snitt i Mathesongården

Det gyldne snitt definerer gårdens størrelse.

Figur 4

Hvis du trekker en linje fra toppen av spiret ned til bakken vil den få lengde 25.2 Dette linjestykkets gyldne snitt er

25.2 * 0.38 = 9.57

som igjen er tilnærmet lik

6 * phi

Lengden fra bygningens front til bakside er 18.9 Dette er så og si lik 2 * høydens gyldne snitt(19.1).

Dersom en går lengden av høydens gyldne snitt ned fra toppen av spiret vil en havne på en høyde som ligger midt imellom kuppelens topp- og bunnpunkt. Dette kan vi vise ved å slå en sirkel med sentrum i dette punktet. (Figur 3)

Figur 5

Slår vi en sirkel med radius lik høydens gyldne snitt med sentrum i kuppelens toppunkt vil den krysse linjen som deler den bakre delen av bygningen i to, samt tangere gulvplanet i tredje etasje.

Figur 6

Vi finner også igjen denne lengden i den bakre delen av bygningen: Trekker vi diagonalene vil de krysses midt i det store vinduet i andre etasje. Avstanden fra krysningspunktet og ut til hjørnene er lik høydens gyldne snitt. (Se fig. 3)

Figur 7

Fra de foregående eksemplene ser vi at høydens gyldne snitt definerer bygningen på et makronivå.

Det gyldne snitt finnes også i detaljene.

Figur 8

I figur 8 har vi tatt et utsnitt av 2de etasje i bygningens bakre del. Utsnittet representerer det midtre av tre rektangler. Den røde linjen har lengde 13, mens de blå har lengde lik den røde linjens gyldne snitt. Det midtre vinduet får altså bredde lik

lengde(rød linje) - 2 * lengde(rød linjes gyldne snitt)

Figur 9

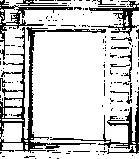
Vinduet i figur 9 har høyde 4 og bredde 2.5 Det er et gyldent rektangel da

a/b = 4 / 2.5

phi = 1.6

Figur 10

Utsnittet i figur 10 har høyde 14 og bredde 4.5 Forholdet mellom sidene blir i dette tilfellet tilnærmet lik 2 * phi

[Forrige: Historikk] [Neste: Etterord]