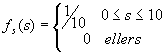
ØVING 6
hentet fra [Matson, 1996, s.150]
Definerer følgende variable:
S er kontinuerlig(antagelse) uniformt fordelt over intervallet (0,10)
S ~ U(0,10)
Tetthetsfunksjonen til en uniformt fordelt variabel er[Dougherty, 1991, s.97] eller [Berck,1992,32.11]
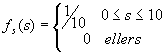
Vi har at x = periodens inntekt til servicebedriften
![]()
Vi definere videre:
xA = Agentens virkelige inntekt i perioden
xP = Prinsipalens virkelige inntekt i perioden
og at
m * = E(X) = forventet periodeinntekt til bedriften.
xA * = E[XA]= Agentens forventede inntekt i perioden
xP * = E[XP]= Prinsipalens forventede inntekt i perioden
UA = Agentens nyttefunksjon
UP = Prinsipalens nyttefunksjon
Fra statistikken vet vi at [Dougherty, 1991,s.112]
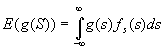
Vi vil klargjøre forskjellen på virkelig og forventet inntekt:
Forventet Inntekt: Agenten vet på forhånd hvor mye han vil få betalt, nemlig 40% av E[X]
Virkelig Inntekt: Agenten vet ikke på forhånd hvor stor inntekten vil bli, siden den er bestemt som 42% av virkelig inntekt.
Når Agenten får en prosentsats av forventet inntekt er man ikke utsatt for ikke-kontrollerbar risiko. Dermed er all denne risiko veltet over på Prinsipalen.
Oppgave 1
Vi skal vise at agentens(A) rasjonelle beslutning er å maksimere uttrykket
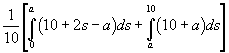
A ønsker å maksimere forventet nytte.Dvs
Maks ![]()
Forventningsverdien av en konstant er en konstant
Maks ![]()
Agenten (A) vil nå maksimere forventet nytte ved å maksimere forventet inntekt ![]()
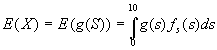
Setter inn tetthetsfunksjonen ![]() for S
for S
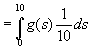
Deler opp integralet, og setter inn for g(s)
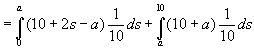
Vi flytter 1/10 på utsiden, og vi har vist det vi skulle.
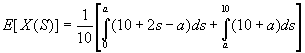
Oppgave 2
Vi må da maksimere forventet periodeinntekt til bedriften E(X)
Max
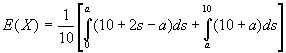
![]()
![]()
Mulige maksimum finner vi ved å derivere dette uttrykket mhp a, og setter det lik 0
![]()
Sjekker om dette er en maksverdi
![]()
Siden dette er et maksimumspunkt, vil optimalt valg av a bli
![]()
Total forventet inntekt for bedriften blir ved a=5 lik
![]()
A skal ha 40% av forventet inntekt ![]()
Forventet nytte til A blir da
![]()
Oppgave 3
Forventet inntekt for P vil være total inntekt minus forventet inntekt betalt til A
![]()
Oppgave 4
Prinsipalen vil få en inntekt som er lik bedriftens virkelige inntekt minus 40% av forventet inntekt
![]()
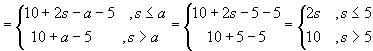
Prinsipalens forventede nytte blir da
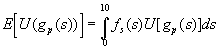
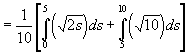
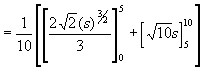
![]()
Oppgave 5
Virkelig inntekt til A:
![]()
Vi må maksimere forventet nytte av 42% av virkelig inntekt
![]()
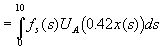
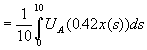
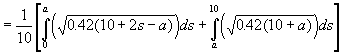
![]() Hvilket skulle vises.
Hvilket skulle vises.
Oppgave 6
Vi finner dette integralet:
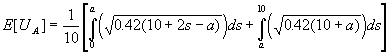
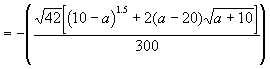
Deriverer dette uttrykket mhp a, setter det lik 0, og får
![]()
Ved å prøve endel verdier fant vi at (HP’en er vår beste venn...)
|
a= |
|
|
4 |
1.16 |
|
4.5 |
-0.0697 |
|
4.45 |
0.0553 |
|
4.4721359 |
0.00000013751 |
![]()
Dette er maksimumsverdien siden den dobbeltderiverte
![]()
er negativ![]()
Maksimum nytte for A er (a=4.4721)
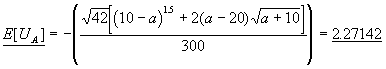
![]()
Når A får 42% av virkelig inntekt vil P få følgende inntekt
![]()
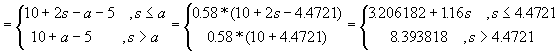
Maksimum nytte for P blir da(![]() )
)
![]()
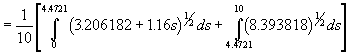
=2.66923
Oppgave 7
Oppsummering:
Når begge parter er risikoaverse(![]() , og
, og ![]() )
)
|
Kontraktsform 1: Agenten får 40 % av forventet inntekt |
Kontraktsform 2: Agenten får 42% av virkelig inntekt |
|
|
Forventet nytte for Agent E[UA] |
|
|
|
Forventet nytte for Prinsipal E[UP] |
|
|
Som vi ser får begge parter øket sin egen nytte ved at kontraktsformen er slik at man deler risiko. I kontraktsform 1, får A en fast inntekt (40% av forventet inntekt), mens A i kontraktsform 2, får en større prosentandel av virkelig inntekt, men som innebærer en risiko på ![]() . Med de gitte nyttefunksjone er de to ekstra prosentene tilstrekkelig for å kompensere for A’s økte risiko. Samtidig reduseres P’s risiko såpass mye at det oppveier den økte forventede utbetaling til A.
. Med de gitte nyttefunksjone er de to ekstra prosentene tilstrekkelig for å kompensere for A’s økte risiko. Samtidig reduseres P’s risiko såpass mye at det oppveier den økte forventede utbetaling til A.
Referanser
[Berck, 1992] Peter Berck og Knut Sydsæter, Matematisk formelsamling for økonomer, Universitetsforlaget, Oslo 1992
[Dougherty, 1990] Edward R. Dougherty, Probability and statistics for the Engineering, Computing and Physical Science, Prentice Hall, London 1990
[Matson, 1996] Einar Matson, Kompendium fag 92008 Bedriftsøkonomi 3, Institutt for økonomi NTH, Trondheim 1996